Weatstone Bridge
The Wheatstone Bridge circuit consists of two potential dividers connected between the supply and ground. One divider is formed from R1 and R2, the other from R3 and R4. The voltage at the point between R1 and R2, and that between R3 and R4 will vary according to the resistor value. Vbridge is the voltage between these points, as shown in the diagram below:
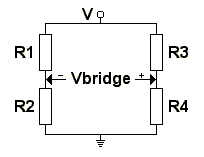
When the voltages are equal Vbridge will be zero, at which point the bridge is said to be balanced. At this point the value of R4 can be found from:
R4 = (R3 * R2) / R1
A typical application for a Wheatstone Bridge is for measuring resistance; if R1 is variable and is adjusted it until Vbridge = 0 the value of R4 can then be found from the above equation.
If all four resistor values (R1 to R4) and the supply voltage (V) are known the voltage across the bridge (Vbridge) can be found by working out the voltage from each potential divider and subtracting one from the other. The equation for this is:
Vbridge = (R4 / (R3 + R4) * V) - (R2 / (R1 + R2) * V)
This can be simplified to:
Vbridge = ((R4 / (R3 + R4)) - (R2 / (R1 + R2))) * V
If the bridge is balanced the equivalent resistance of the circuit between V and GND is:
R1 + R2 in parallel with R3 + R4
RE = ((R1 + R2) * (R3 + R4)) / (R1 + R2 + R3 + R4)


